未来研通信

来週の日曜日

みなさんこんにちはFUJITAです。

来週の日曜日(19日)、「第２８回全国１位争奪戦　C1エリア」が終了します！
(週の始まりは「日曜日」！)

お気に入りのネームプレートはゲットできましたか？

そのネームプレートの中にあった、こちら、

ネームプレート「答案用紙」

「正解はなんなんだよ！」という方もいる？と思うので解いてみましょう！

問題としては「角Xの角度を求める」ですね。
スペースの都合で？書かれていませんが、右下の角を「C」としましょう。

∠Aは76°

三角形の内角の和は180°なので、∠B + ∠Cは180°- 76°＝104°

∠●は∠Bの半分、∠#は∠Cの半分です。

∠B + ∠C = ∠● + ∠● + ∠# + ∠# = 104°なので、∠● + ∠# = 52°

△PBCにおいて、∠X + ∠● + ∠# = 180°で、∠● + ∠# = 52°なので、

∠X = 180°- 52° = 128°

A．128°

でした！

ところで、この問題のように「三角形の各角の二等分線の交点」のことを「内心」といいまして、
内接円の中心と同じになります。

「内心」があるなら「外心」もあるだろう！ということで、

三角形の各辺の中点を通る垂線の交点を「外心」といい、その三角形の外接円の中心と同じです。

で、「車界隈」でよく聞く「重心」ですが、

三角形の重心は、各辺の中点と対角の頂点を結んだ各線の交点が「重心」となります。

何事も「重心は低く」が基本ですｗ

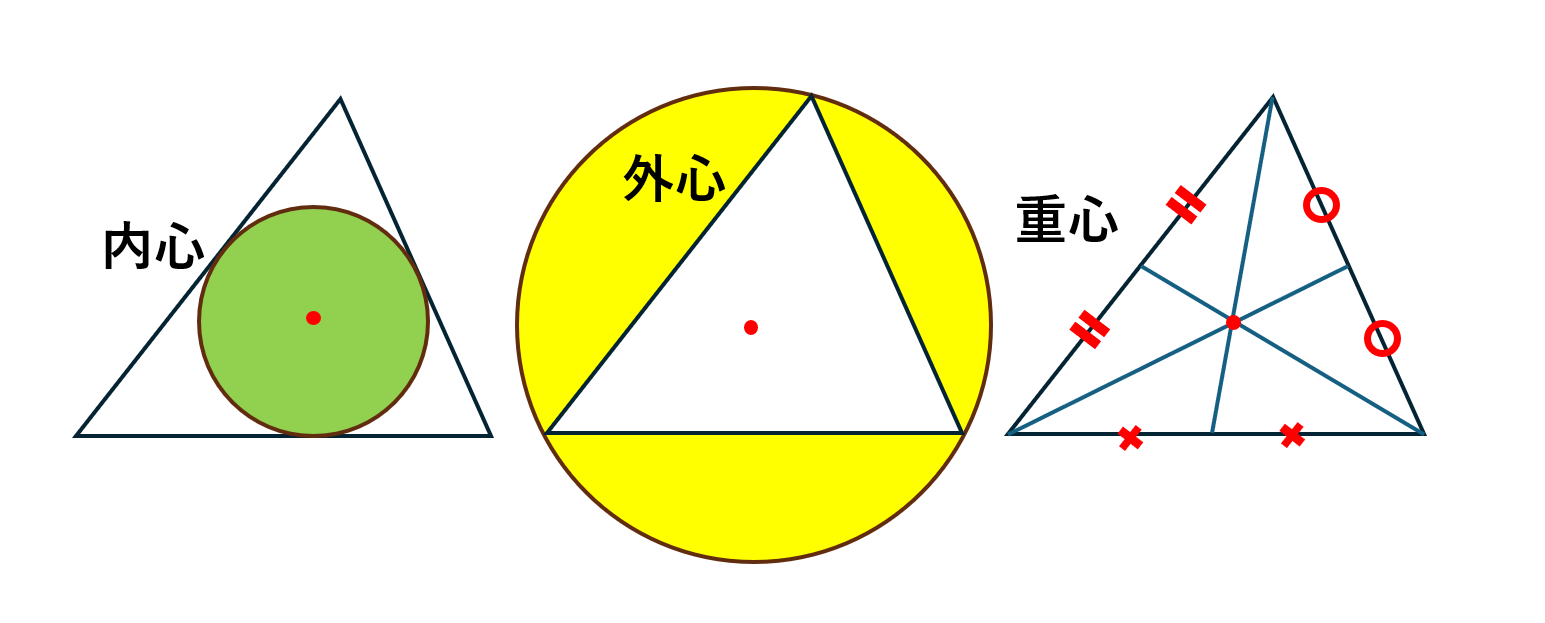
「内心」「外心」「重心」、同じように見えるかもしれませんが、微妙に違います。

ところで、三角形には「三角形の5心」という概念がありまして、あと「2心」は何？ということで興味ある人は調べてみよう！

再来週の日曜日

再来週の日曜日(26日)は、

「湾岸マキシ タイムアタック認定会 IN 京都(第2回)」

が、開催されます！お近くの方はぜひお立ち寄りください！初"心"者も大歓迎ですよ！

すっかり涼しくなってきたところですが、まだまだ熱い走りを見せてくれ！

というわけで、以上「心が大事」というお話でした...？

それではまた～。