第55回
2025/06/04

FUJITA
みなさんこんにちはFUJITAです。
湾岸マキシが好きでよく遊んでくれている皆さんの中には、将来「AIプログラマー」や「車関連のエンジニア」なんかになりたいぜ!と思っている中高生さんが少なからずいますよね?ね??いっぱいいますよねw
そんな、理系の道へ進もうとしているあなたに、今日はFUJITAから数学のお勉強をプレゼントしたいと思います。
(たまにむねかたが「物理学」的なことの話をするので、対抗したいと思います!!)
では早速。
湾岸マキシに登場するMAZDA車に多く採用されている「ロータリーエンジン」において、
その回転ピストンは「ルーローの三角形」ですが、ルーローの三角形の面積を求めてみましょう!
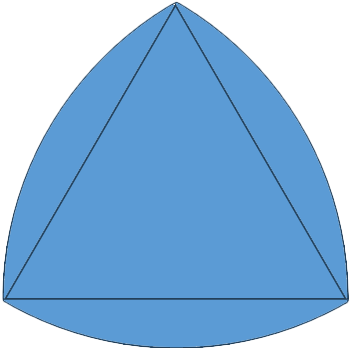
ここで「ルーローの三角形」を定義しておきます。
「正三角形を1つ用意して、その正三角形の1辺の長さを半径とする円を、その3つの各頂点を中心として描き、その正三角形を、描かれた弓型で囲んだ図形。」とします。(下図の青い部分)
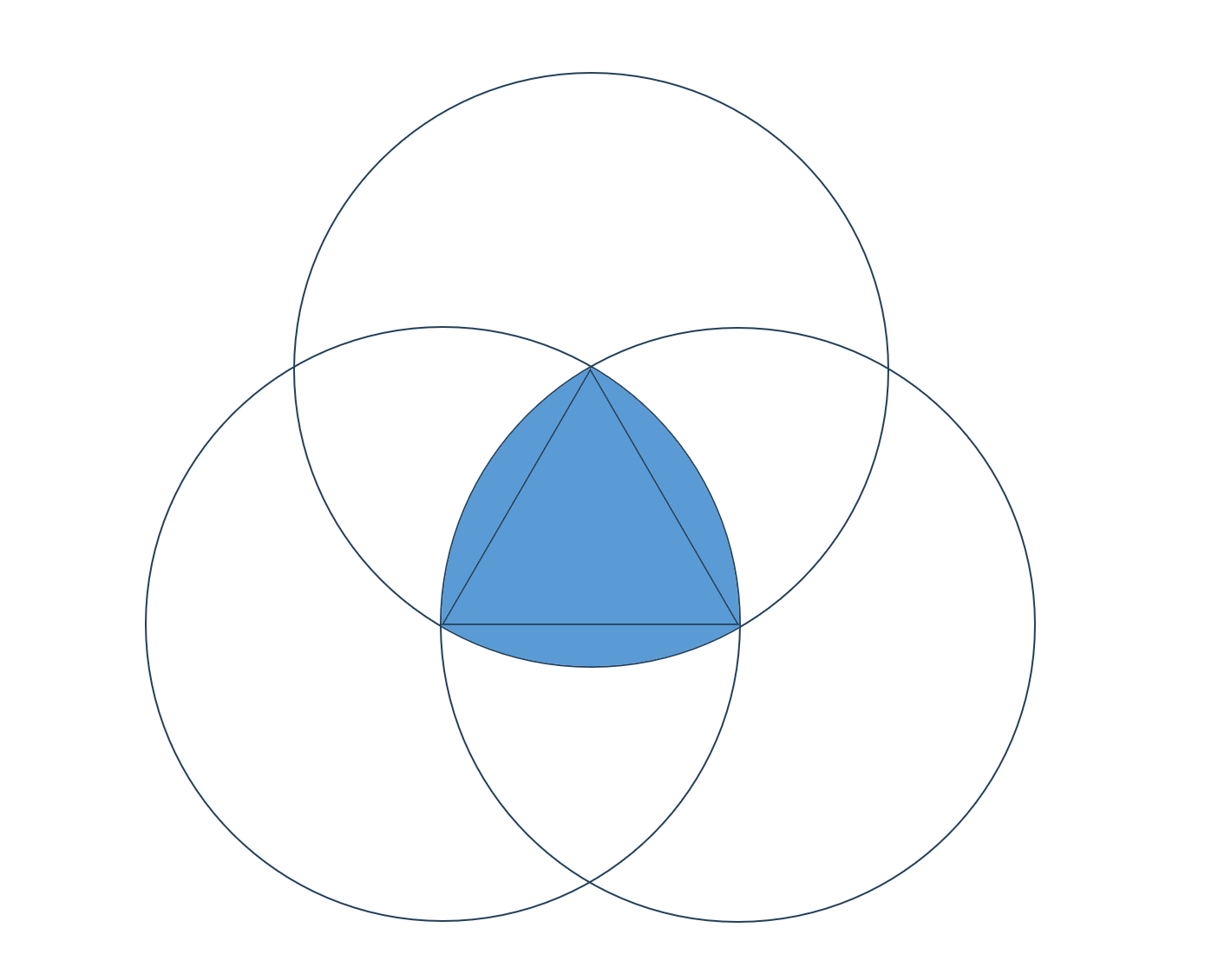
【問題】
1辺の長さ「1」の正三角形部分からなる、ルーローの三角形の面積を求めよ!
【解法】
正三角形の1辺の長さを「1」とすると、ルーローの三角形の面積は、
「正三角形1つの面積 + 弓型部の面積3個の合計」になるので、まずは正三角形の面積を求めると、
「三角形の面積:底辺×高さ×1/2」から、
となります。
※ここで、1辺の長さ「1」の正三角形の「高さ:√3/2」をどうやって導くかと言うと、「三角定規」の「3つの角が90度,60度,30度の方(90度、45度、45度じゃない方)の3辺の比が、2:1:√3であることを使用しました。(もちろん三角関数使ってもいいです。)
次に弓型の面積を求めたいところですが、ちょっと面倒臭そうなので工夫しましょう。
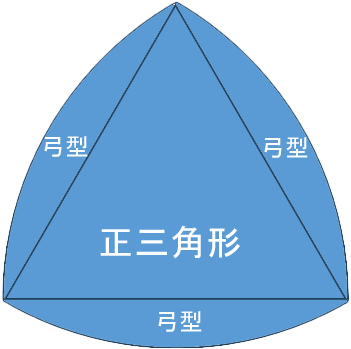
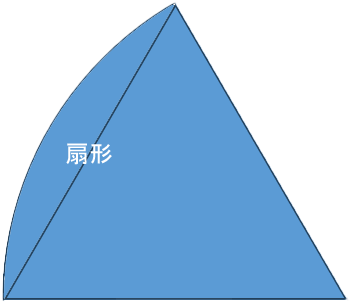
ルーローの三角形の面積は、「扇形3つ分から正三角形2つ分を引いた面積」となり、また「扇形3つ分」は、ちょうど「半円」なので、
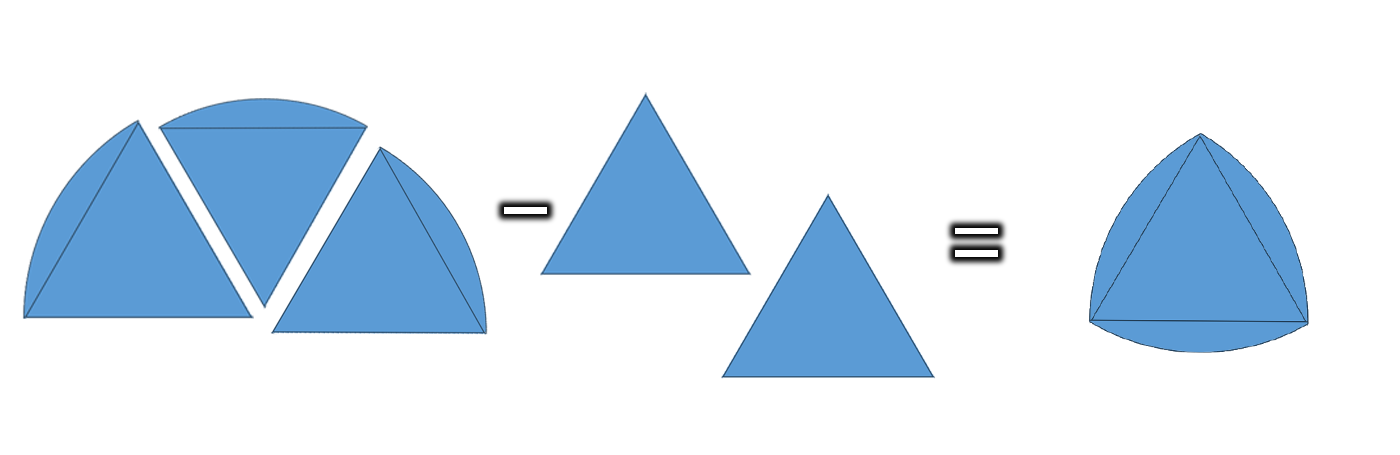
円の面積は、半径×半径×円周率(π)ですから、
半円なので、
ここから正三角形2個分引くと、
【答え】
以上、意外とすっきりした答えになりましたね~。
将来のエンジニア諸君には簡単すぎたかな!?では次回はもうちょっと難しい問題を出しましょう!(いいネタを探さねば汗)
それではまた~!
