未来研通信

みなさんこんにちはFUJITAです。

前回は、将来のエンジニアさんに向けて数学の問題をプレゼントしましたが、大好評につき第2弾！をお届けしたいと思います！
「簡単すぎだ！ナメてんのか！！」の声に応えて、今回は少々レベルUP!しますよ～。

前回は「ルーローの三角形」だったので、三角形つながりで「三平方の定理／別名：ピタゴラスの定理の証明」をしたいと思います！

「三平方の定理」は中学三年生で習うので、知っている人も多いと思いますが一応確認。

三平方の定理（ピタゴラスの定理）とは？

直角三角形の３辺をa、b、c（c斜辺）とするとき、

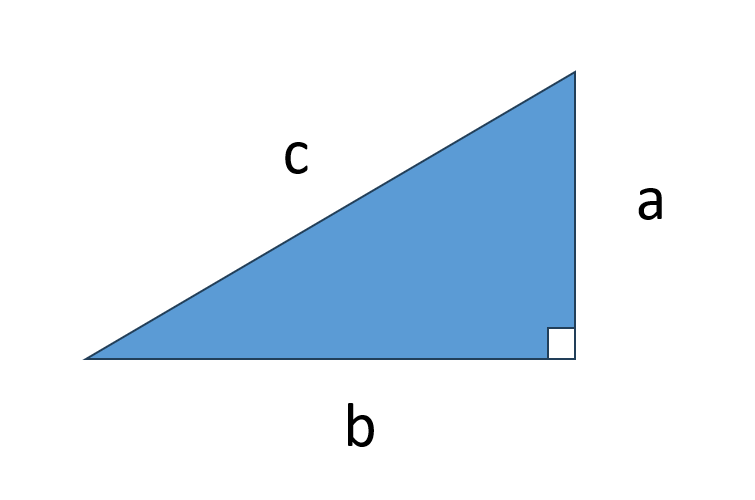
$$a^{2} + b^{2} = c^{2}$$

が成り立つ、というものです。

三平方の定理（ピタゴラスの定理）の証明

４つの同じ直角三角形を下図のようにならべて、できた図形の面積を考えます。

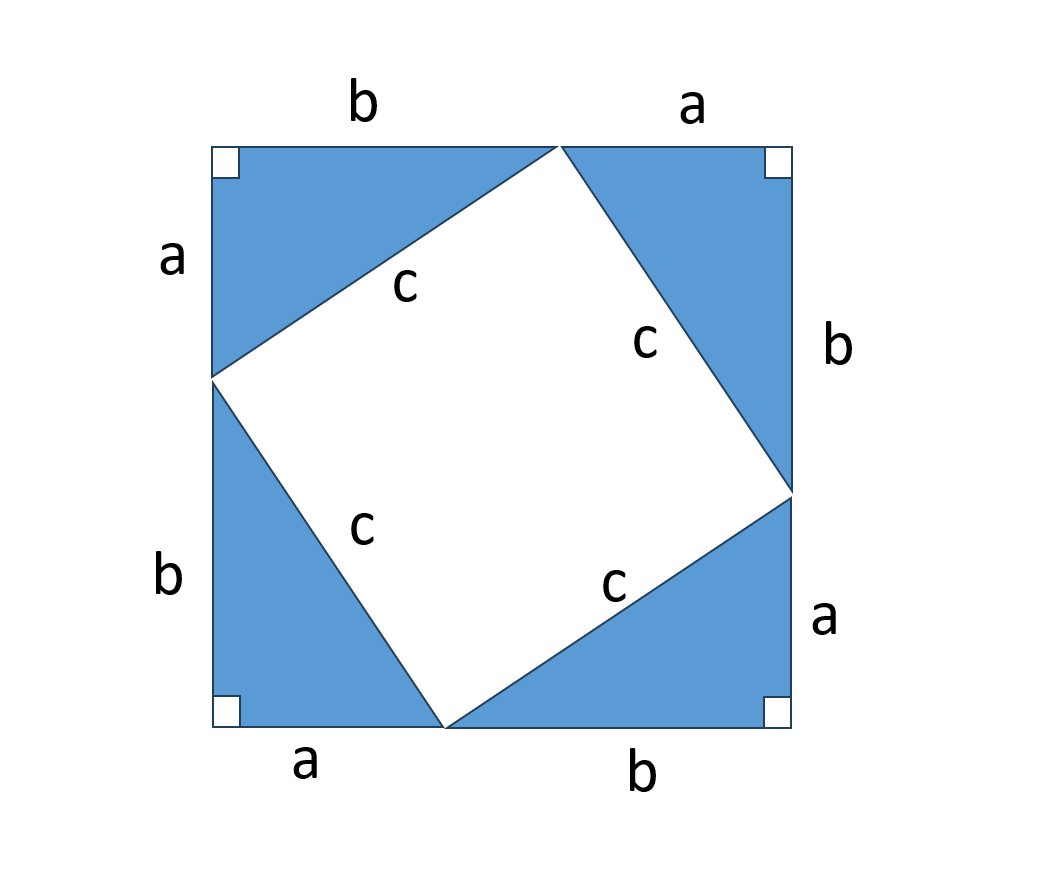
外側の大きい正方形の面積は、一辺がa+bなので、

$$(a + b) \times (a + b) = {(a + b)}^{2}$$... (1)

となります、

一方、同じ図で「４つの三角形」と「内部の斜めの小さい正方形」の合計も「外側の大きい正方形の面積」と同じです。

式にすると、

三角形の面積は「底辺×高さ÷２」なので、

$$a \times b \div 2 = \frac{ab}{2}$$

三角形は４つあるので４倍して、

$$\frac{ab}{2} \times 4 = 2ab$$

です。

また内部の斜めの小さい正方形の面積は、一辺がｃなので、

$$c \times c = c^{2}$$

です。合計して、

$$2ab + c^{2}$$ ... (2)

(1) と(2)は等しいので、

$${(a + b)}^{2} = 2ab + c^{2}$$

となります。これを整理します。左辺を展開して、

$$a^{2} + {2ab + b}^{2} = 2ab + c^{2}$$

両辺に同じ「2ab」があるので、それぞれ消して、

$$a^{2} + b^{2} = c^{2}$$

となり、三平方の定理の公式が導けましたので証明終わり！

三平方の定理の証明方法は500種類以上あるらしい？ので、興味がある人はほかの方法も考えてみよう！

最近だと、アメリカの10代の2人の少女が新しい証明方法を発見したというニュースが、「ピタゴラス界隈」で話題になったのは記憶に新しい...よな！なｗ

さて、突然ですが！人類がこの先滅びることなく持続生存していく方法は（急に重ｗ）、新しいテクノロジーで「今までできなかったことができるようになる」ということがその１つだとおじさんｗは思います。

無限の可能性を秘めた、理系女子・男子の若者達よ（文系女子・男子もね！）、未来は君たちの手にかかっているよ！

それではまた～。